摘要:在本文中,我們研究了基于紅外熱成像的印制電路板故障檢測中的圖像配準問題。為了提升印制電路板紅外熱成像的質量,本文提出了一種新穎的預處理方法,該方法能夠保證圖像配準的效果。由于印制電路板紅外熱成像與常見的圖像存在顯著差異,鮮有現有的圖像配準研究專注于印制電路板紅外熱成像配準。因此,本文對比了多種配準算法,以尋找適用于不同檢測方法的印制電路板紅外熱成像配準算法。結果顯示,基于互信息的配準方法更加精確但計算量大,適用于熱成像序列檢測;而基于SIFT特征的配準方法效率更高,但精度較低,適用于熱成像差分檢測方法。
1 引言
隨著技術的發展,印制電路板上的組件和電路正朝著精細化、高密度化和復雜化的方向發展。[1-3] 板子越復雜,成本也就越高。因此,在印制電路板的發展過程中,故障檢測與維護已經成為我們必須面對的問題。傳統的手工檢測方法已經難以滿足現今的檢測需求。作為一種非接觸式的測量方法,紅外熱成像檢測逐漸應用于印制電路板故障檢測領域。基于紅外熱成像的印制電路板故障檢測主要包括三個步驟:熱源識別、特征提取及熱圖模式識別[4]。本文重點關注在熱源識別過程中的圖像配準問題。由于現有的檢測方法都需要比較印制電路板正常工作狀態下和發生故障時的紅外熱成像中組件的狀態,因此必須對這兩種狀態下的印制電路板紅外熱成像進行配準,以實現組件的配準。只有在兩張印制電路板的紅外熱成像圖完成配準后,后續的檢測步驟才能進行。印制電路板圖像的配準效果將直接影響故障檢測的準確性。
學者們對印制電路板的熱圖像配準進行了一系列的研究。在文獻[5]中,提出了一系列圖像配準的方法。而在文獻[6]中,則使用了遺傳算法來實現印制電路板的熱圖像配準。但是,現有的研究仍然缺乏針對性。因為印制電路板熱圖像配準是后續檢測的基礎,所以有必要綜合考慮印制電路板熱圖像檢測方法和配準方法,并根據不同的基于紅外熱成像的印制電路板檢測方法找到更合適的配準方法。在本文中,研究了印制電路板熱圖像配準的預處理和配準方法。
2 問題描述
2.1 圖像配準定義
圖像配準意味著在相同場景和不同拍攝環境下,在多幅圖像之間建立對應關系,以使多幅圖像之間的像素對齊[7-9]。兩幅圖像可能是在不同時間拍攝的,甚至可能來自不同的傳感器,并且相機可能處于不同的拍攝位置。從數學上講,兩幅圖像的配準可以定義為:
I2(x,y)=L(F(I1(x,y)))
其中, I1 和 I2 分別代表需要配準的圖像,例如,正常狀態下的印制電路板熱成像圖和故障狀態下的印制電路板熱成像圖。 和 分別表示這兩幅圖像在位置 上的灰度值,L?表示一維灰度變換函數,而 F?表示二維空間幾何變換函數。
目前,有兩種常見的基于紅外熱成像的印制電路板故障檢測方法[10]:熱成像差分檢測方法和熱成像序列檢測方法。熱成像差分檢測方法通過從故障狀態下的印制電路板瞬態熱圖像中減去正常狀態下的印制電路板熱圖像來檢測組件故障。這種方法適用于故障實時預警,因為它可以快速定位和顯示故障。該方法的缺點是無法檢測那些隨著時間緩慢變化溫度的故障。故障檢測的準確性直接取決于圖像配準的準確性,因此圖像配準在差分檢測中起著重要作用。
另一種方法是熱成像序列檢測。首先,需要在正常工作條件下的印制電路板熱圖像序列和故障條件下工作的印制電路板熱圖像序列中識別出熱源。然后,需要從這兩個序列中提取各自組件的溫度變化信息。通過比較兩種溫度變化信息來檢測每個組件,確定是否存在故障。這種順序熱成像檢測方法用于識別正常工作狀態下和故障狀態下印制電路板熱圖像序列中的熱源,并提取正常工作狀態和故障狀態下的各組件溫度變化信息。通過比較這兩種變化信息來檢測每個組件是否出現故障。這種方法的優點是可以檢測復雜的電路故障,而缺點是效率較低。組件配準的準確性將直接影響溫度變化信息的提取。因此,組件配準在這種方法中也起到了重要的作用。
3 印制電路板紅外熱成像的預處理
印制電路板紅外熱成像具有高噪聲、低對比度和邊緣模糊的特點[11]。這些特性阻礙了特征信息的提取,并會影響印制電路板紅外熱成像的配準。因此,在紅外熱成像檢測中對印制電路板熱圖像進行預處理是必要的。
由于印制電路板紅外熱成像通常包含大量的椒鹽噪聲,中值濾波方法可以有效地去除椒鹽噪聲,因此采用此方法去除噪聲。
為了充分利用印制電路板熱圖像中的線條、角落等特征信息,可以使用Prewitt算子來提取印制電路板熱圖像中組件的邊緣輪廓信息,這可以銳化組件的邊緣。該算子的優勢在于它不僅可以提取邊緣,還可以減少噪聲的影響。相應的Prewitt算子的卷積模板和形式如下:
對于水平邊緣檢測,Prewitt算子的模板為:
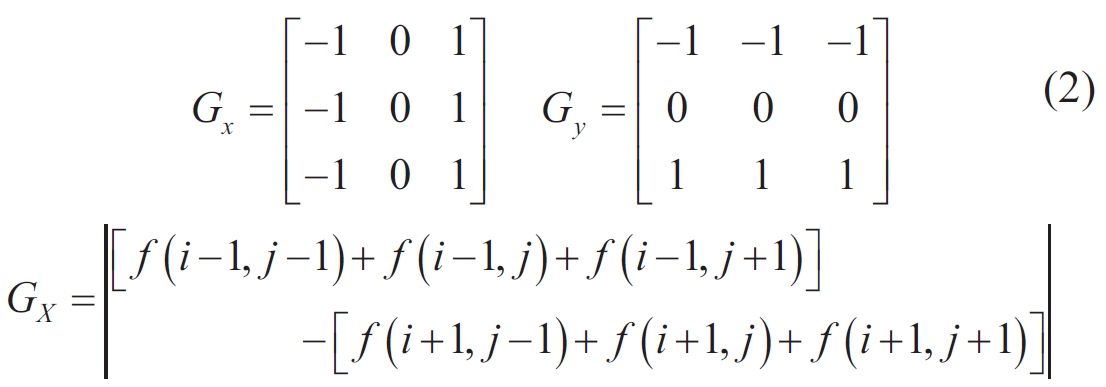
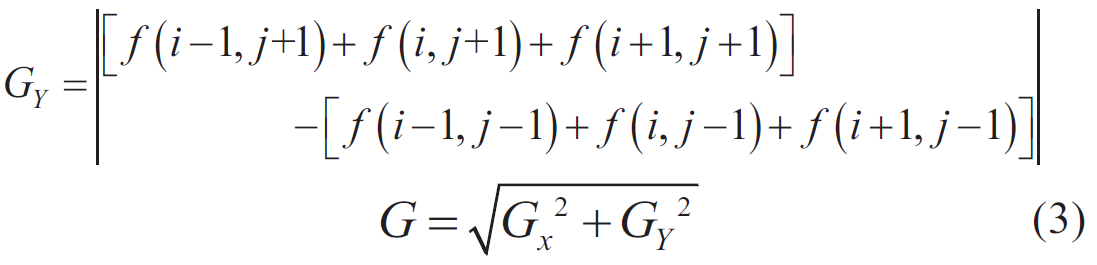
其中 GX 和 是卷積運算符,而 f(i,j)?表示成像。為了在印制電路板紅外熱成像中突出故障組件區域,可以使用直方圖均衡化方法來處理圖像。這種操作可以使組件區域變得更亮,而背景區域變得更暗,從而實現突出組件的目的。直方圖均衡化的變換公式如下:
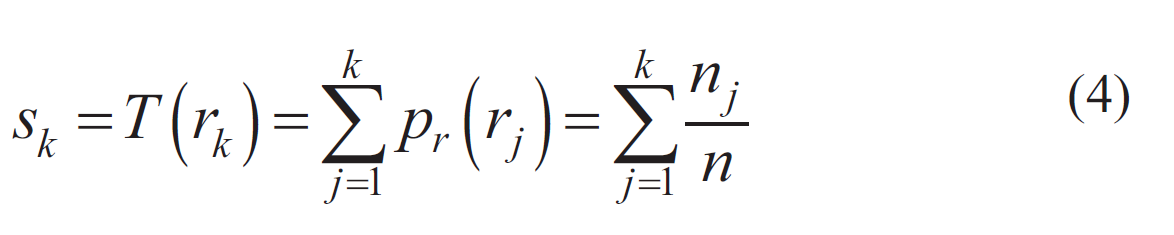
其中 k=1,2,…,256,ks 意味著均衡化處理后的灰度值,而 代表直方圖均衡化前的成像灰度值。
在本文中,印制電路板熱圖像的增強和預處理如下:使用中值濾波去除噪聲,使用Prewitt算子銳化邊緣,使用直方圖均衡化來提高對比度。在本文中,使用添加了噪聲的印制電路板熱圖像來模擬實際獲取過程中的印制電路板熱圖像。實驗結果如下所示。圖像平均灰度值、信息熵和方差有了顯著提高,而峰值信噪比、均方誤差則不理想。但是可以看出增強圖像的組件邊界更清晰,整體圖像質量得到了改善,這證明了對印制電路板紅外熱成像的預處理提高了成像質量。

a原始印制電路板紅外熱成像

b添加了噪聲的印制電路板紅外熱成像

c經過預處理的印制電路板紅外熱成像
圖1:增強效果的對比
表1:評價指標的比較
| 指標 | 添加噪聲成像 | 預處理后成像 |
| 平均灰度值 | 120.6013 | 127.9997 |
| 信息熵 | 6.7328 | 7.0892 |
| 方差 | 4.68E+03 | 5.44E+03 |
| 均方誤差(MSE) | 24.8662 | 115.8539 |
| 峰值信噪比(PSNR) | 34.1747 | 27.4917 |
4 圖像配準方法
4.1 基于互信息的配準算法
互信息是一種數學定義,用來評估隨機變量之間的關聯性。它表示兩個隨機變量中的共有信息。由信息熵描述的互信息表達式如下[12]:
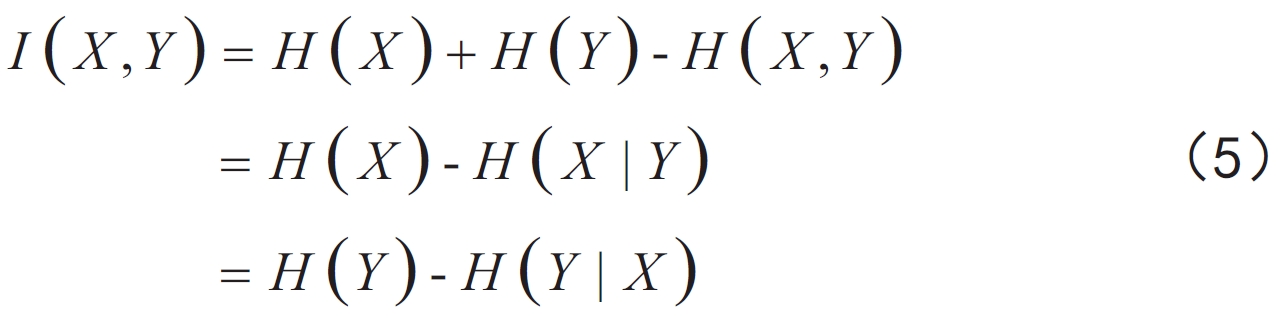
其中 H(X)?是 X 的熵, 是 的熵, 是 和 的聯合熵, 是給定 Y時 X 的條件熵, 是給定 時 的條件熵。 和 是隨機變量,可以代表紅外熱成像圖像。
基于最大互信息理論,可以得出結論,當故障印制電路板紅外熱成像與正常印制電路板紅外熱成像匹配時,兩幅熱圖像的互信息值達到最大值。這解釋了為什么互信息可以用于圖像配準。印制電路板紅外熱成像之間的互信息可以如下計算:
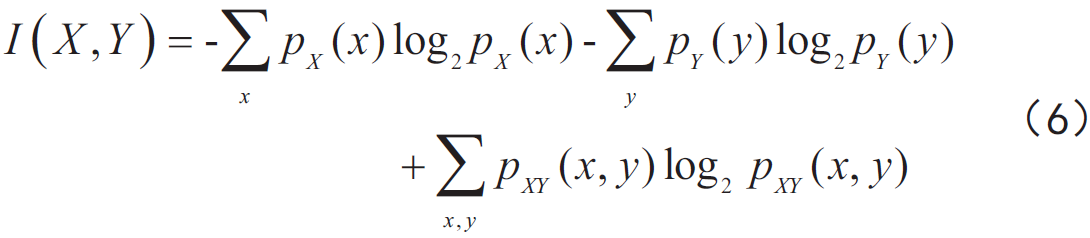
印制電路板紅外熱成像之間的互信息
其中 ( p(x) ) 和 ( p(y) ) 分別代表紅外熱成像 ( X ) 和紅外熱成像 ( Y ) 的概率分布函數,( p(x, y) ) 代表紅外熱成像 ( X ) 和紅外熱成像 ( Y ) 的聯合概率分布函數。所有這些都可以從兩幅紅外熱圖像的組合分布直方圖中獲得。公式的另一種表達方式是:
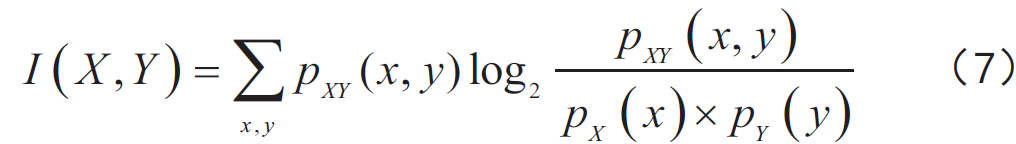
印制電路板紅外熱成像之間的互信息
![[靈蜂智能官網]-專業紅外熱像儀廠家](http://linfun.com.cn/wp-content/uploads/2022/06/2022060807191642.png)
![[靈蜂智能官網]-專業紅外熱像儀廠家](http://linfun.com.cn/wp-content/uploads/2021/10/202110130602107.png)