熱組件的建模
如圖5所示,熱網絡可以被視為一系列集總電阻和電容模型的串聯,每個集總組件的時間常數τ = R × C,其中C為熱容,R為熱阻。只要這些時間常數彼此之間足夠分離,熱網絡電路可以類比為一個電氣RC電路,作為福斯特(Foster)梯形而非考爾(Cauer)梯形。福斯特梯形(式1)由每個電阻和電容并聯組成一個組件,然后這些組件串聯連接。福斯特梯形更容易對熱網絡進行建模,而后者則反映了熱容組件的物理連接。
![]()
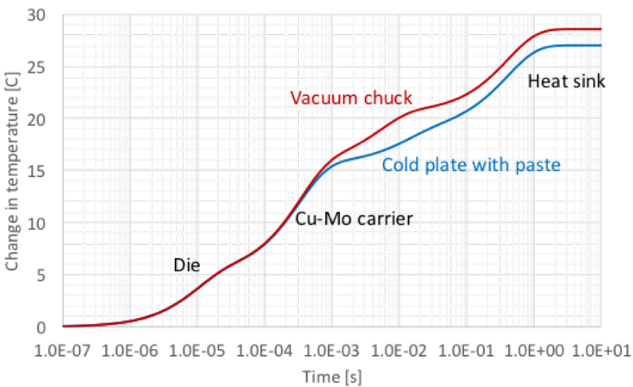
其中,θ表示溫度變化,t表示時間,τ表示第 i個組件的時間常數。圖4展示了一個仿真示例,說明了由于芯片接觸差異而導致的瞬態響應差異,而其他組件完全相同。上部曲線由于干接觸造成的不良接觸而具有更高的熱阻,下部曲線由于使用了熱膏,通過填充微觀空隙提供了更好的接觸,因此具有較低的熱阻。
更精確的瞬態響應建模將有助于在達到穩態時準確識別每個電阻組件。對于時間上有更多重疊的更復雜系統,可以通過使用RC積分的分解方法來找到累積結構函數。這種分解可以通過使用時間響應函數等數學方法完成,例如參考文獻 [7]。
圖5展示了模擬的時間響應。該模型假設熱阻分別為:芯片 5.1 [K/W]、銅鉬載體 10.5 [K/W]、散熱器 8 [K/W]。對于干接觸(使用真空吸盤)的熱阻為 5 [K/W],而帶有膏狀材料接觸的熱阻為 2.7 [K/W],其中膏狀材料的界面熱阻為 0.1 [K/W]
亞衍射成像
上述納米特征要求溫度場的空間分辨率達到100納米以下,而可見光的波長大于360納米。根據瑞利分辨率準則,兩個點狀物體可以在距離D(從點源的半徑)處被分辨,該距離D由下式給出 [8]:D=1.22λ/sin?(α)
這里, 是物鏡的f數,而 λ 是從表面反射回來的光的波長。 大約等于,其中 N.A. 是透鏡的數值孔徑。式 (2) 通常被稱為衍射極限。
我們正在測量一個比距離 D 小的器件寬度。因此,這是一個亞衍射極限特征。這個系數來自于從點源發出的能量譜作為距離的函數。圖6中的艾里盤確定了能量譜在貝塞爾函數輪廓中為零的距離極限,這是以點源為中心的距離函數 [9]。這個能量輪廓在艾里盤內可以用高斯輪廓近似擬合,其系數為 2.44,這便于進一步的數學處理。從點源沿距離的能量譜可以描述為:
E(r)=E0f(r)
其中:
- 是距離點源??處的能量強度;
- ?是最大能量強度;
- 是隨距離??變化的函數,這里可以用高斯函數近似。
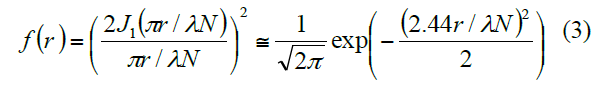
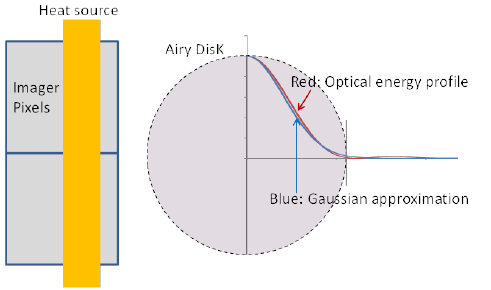
圖6展示了熱源與成像系統的相對位置。熱源的寬度遠小于成像像素的尺寸以及艾里盤的直徑,這意味著需要使用亞衍射成像技術才能實現足夠的空間分辨率來準確捕捉熱源的溫度分布。此外,加熱線與像素行的平行但不對齊意味著熱源的圖像可能會跨越多個像素,從而影響成像質量。一般情況下,線熱源可以通過二維對稱性(均勻熱擴散)來估算。在截面平面中,基底中的熱擴散作為時間的函數可以用無限半空間中的Bessel函數來表示。我們可以根據Yovanovich的方法使用閉式解 [10]。因此,點源的集成,它們各自具有依賴于局部溫度的反射能量譜,最終成為光子能量譜。最后,這一強度譜被映射到成像器中的成像像素上,并進行數學計算。通過將反射強度與無限分辨率下的強度進行比較,最終可以找到熱反射系數。光學CCD圖像比較圖7展示了1微米和100納米線熱源裝置之間的光學CCD圖像比較。1微米線熱源清晰可見,而100納米線在530納米波長的照明下模糊且難以識別。數值熱模擬結果圖8展示了偏置條件下的數值熱模擬結果。圖8a顯示了使用有限元方法計算的真實溫度分布。圖8b是一個過濾后的結果,使用了艾里盤內的高斯函數(系數為2.44,半徑為353納米)。這張圖像代表了我們期望通過特定光學系統獲得的圖像,并與圖8c中顯示的實際圖像進行了比較。區域遠小于芯片的尺寸,熱膨脹會在XY平面上以及沿深度方向引起顯著的位移,這會妨礙準確獲取正確的熱信息。為此,使用了一個三維壓電階段控制器來穩定視野中的聚焦位置。逐像素地獲取熱反射系數使得可以從目標位置精確地重新檢測到光強度,參見 Ref [6]。
![[靈蜂智能官網]-專業紅外熱像儀廠家](http://linfun.com.cn/wp-content/uploads/2022/06/2022060807191642.png)
![[靈蜂智能官網]-專業紅外熱像儀廠家](http://linfun.com.cn/wp-content/uploads/2021/10/202110130602107.png)